Tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp

Tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp

Bài viết hôm nay, thcs Hồng Tháibook.com sẽ giới thiệu cùng quý thầy cô và các bạn học sinh chuyên đề tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp. Hi vọng, đây sẽ là nguồn tư liệu hữu ích giúp các bạn dạy và học tốt hơn. Cùng chia sẻ ngay thôi nào !!!

Bạn đang xem: Tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp

I. LÝ THUYẾT VỀ TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

1. Khái niệm và tính chất

Bạn đang xem: Tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp

2. Biểu thức tọa độ của tích vô hướng

Trên mặt phẳng tọa độ  cho hai vec tơ . Khi đó tích vô hướng  và  là:

Nhận xét: Hai vectơ khác vectơ  vuông góc với nhau khi và chỉ khi:

3. Ứng dụng

a) Độ dài của vectơ: Độ dài của vec tơ  được tính theo công thức:

b) Góc giữa hai vec tơ: Từ định nghĩa tích vô hướng của hai vec tơ ta suy ra nếu  khác vectơ  thì ta có:

c) Khoảng cách giữa hai điểm: Khoảng cách giữa hai điểm  được tính theo công thức :

II. CÁC DẠNG TOÁN THƯỜNG GẶP CỦA TÍCH VÔ HƯỚNG CỦA HAI VECTƠ

Dạng 1: chứng minh Hai vecto vuông góc

A. Phương pháp giải

Phương pháp 1: Sử dụng định nghĩa

Nếu  thì hai vectơ  vuông góc với nhau, kí hiệu .

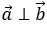
Phương pháp 2: Sử dụng tính chất của tích vô hướng và áp dụng trong hệ tọa độ

Cho .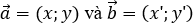

Khi đó:

B. Ví dụ minh họa

Xem thêm : 99+ Hình nền cute phô mai que đẹp cho điện thoại

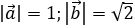
Ví dụ 1: Cho hai vectơ  vuông góc với nhau và . Chứng minh hai vectơ  vuông góc với nhau.

Hướng dẫn giải:

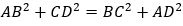
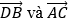
Ví dụ 2: Cho tứ giác ABCD có . Chứng minh hai vectơ  vuông góc.

Hướng dẫn giải:

Ví dụ 3: Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC và điểm D bất kỳ thuộc cạnh AC. Tính AD theo a để BD ⊥ AM.

Hướng dẫn giải:

Dạng 2: Tìm m để góc giữa hai vecto bằng một số cho trước (45 độ, góc nhọn, góc tù)

A. Phương pháp giải

Các bước làm bài

B. Ví dụ minh họa

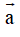
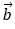
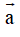
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ  = (3;m) và  = (1;7). Xác định m để góc giữa hai vectơ  và  là 45°.

Hướng dẫn giải:

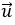
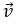
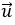
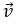
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho hai vectơ  = (-1;1) và  = (m;⁡2). Tìm m để góc giữa hai vectơ  và  là 135°.

Hướng dẫn giải:

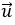
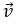
Vậy không tồn tại m để góc giữa hai vectơ  và  là 135°.

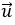
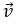
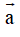
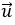
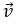
Ví dụ 3: Trong mặt phẳng tọa độ Oxy cho hai vectơ  = (4;1) và vectơ  = (1;4). Tìm m để vectơ =m. +  tạo với vectơ  một góc 45°.

Hướng dẫn giải:

Đáp án C

III. BÀI TẬP VẬN DỤNG

1. Cho hai vectơ’ a và overline{mathrm{b}}. Chúng minh rằng:

2.Cho hai vectơ  có  và .Tính tích vô hướng 

và suy ra góc giữa hai vectơ a và 

3. Cho tam giác đều ABC canh a. Goi H là trung điểm BC,tính

4. Cho hình vuông ABCD tâm O,cạnh a.Tính:

b) OA .AC

c) AC. CB

5. Tam giác , tính AB.AC

6. Tam giác ABC có AB =5, AC =4, 

a)tính 

7. Tam giác ABC có 

a)Tính  rồi suy ra giá trị góc A

b)Tính CA . CB

Vậy là các bạn vừa được tìm hiểu chuyên đề tích vô hướng của hai vectơ: lý thuyết và bài các dạng bài tập thường gặp. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu phục vụ quá trình dạy và học được tốt hơn. Xem thêm cách giải phương trình bậc bốn tại đường link này nhé !

Đăng bởi: thcs Hồng Thái

Chuyên mục: Giáo dục

Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!

Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)