Thế nào là 2 góc phụ nhau và 2 góc bù nhau? – Tin Đẹp

Góc phụ nhau là hai góc có tổng giá trị bằng 90 độ. Khi hai góc phụ nhau được gắn với nhau, chúng ta có thể tạo ra một góc vuông. Góc phụ nhau có nhiều ứng dụng trong toán học và hệ thống tọa độ, nhất là trong việc tìm giải pháp cho các bài toán về hình học.

Ví dụ, trong hình chữ nhật, hai góc cạnh song song có tổng là 90 độ là góc phụ nhau. Nếu chúng ta cần tính toán góc giữa hai đường thẳng, chúng ta có thể sử dụng góc phụ nhau để giải quyết bài toán này.

Bạn đang xem: Thế nào là 2 góc phụ nhau và 2 góc bù nhau? – Tin Đẹp

Tổng quan, góc phụ nhau là một khái niệm quan trọng trong toán học và hệ thống tọa độ, và có rất nhiều ứng dụng trong các lĩnh vực khác nhau, như kỹ thuật, xây dựng và công nghiệp.

Bài viết này, tindep.com sẽ giới thiệu đến các bạn tính chất cộng của góc và một số khái niệm về 2 góc kề nhau, 2 góc phụ nhau, 2 góc bù nhau. Bên cạnh đó là một số bài tập liên quan có lời giải chi tiết để giúp các bạn nắm được phương pháp giả các bài toán liên quan về góc. Chúng ta cùng nhau bắt đầu tìm hiểu về kiến thức Toán học ngay bên dưới nhé.

Tìm hiểu tính chất cộng của góc

Khi nào thì góc xOy + yOz = xOz ?

Để biết được câu trả lời thì trước hết ta hãy tìm hiều ví dụ sau:

Cho góc xOz = 120. Tia Oy nằm trong xOz . Hãy đo các góc yOz, xOy và sau đó rút ra nhận xét?

Ta vẽ góc xOy = 120, sau đó vẽ tia Oy nằm bên trong góc này. Khi đó, sẽ có 2 trường hợp xảy ra

Trường hợp 1: Khi mà hai góc zOy và yOx khác nhau. Giả sử trong trường hợp này thì ta đo được góc yOz = 30, góc còn lại góc xOy = 90.

Trường hợp 2: Chúng ta sẽ xoay tia Oy, sau đó ta đo góc zOy và góc xOy đều bằng 60.

Chúng ta cùng nhìn lại hai trường hợp thì sẽ rút ra được:

Nếu tia Oy nằm giữa hai tia Ox và Oz thì ta có tính chất cộng góc xOy + yOz = xOz , ngược lại nếu ta có tính chất cộng góc xOy + yOz = xOz thì ta khẳng định được tia Oy nằm giữa hai tia Ox và Oz.

Thế nào là hai góc kề nhau, phụ nhau, kề bù?

Nếu hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh chung thì hai góc đó được gọi là hai góc kề nhau.

2 góc phụ nhau là gì? Hai góc phụ nhau là hai góc có tổng số đo bằng 90. Ví dụ như các góc 40, 50, đó là hai góc phụ nhau.

2 góc bù nhau là gì? Góc bù nhau là 2 góc có tổng số đo bằng 180 độ.

Nếu hai góc có tổng số đo bằng 180 thì hai góc đó phụ nhau. Ví dụ như các góc 60, 120 , đó là hai góc bù nhau.

Các bạn cần chú ý để tránh nhầm lẫn hai góc phụ nhau và hai góc bù nhau.

Hai góc được gọi là hai góc kề bù nếu như chúng vừa kề và vừa bù với nhau. Nghĩa là chúng có cạnh chung, hai cạnh tương ứng nằm ở hai phía mặt phẳng bờ là cạnh chung và tổng số đo của chúng là 180.

Bài tập về hai góc phụ nhau, bù nhau

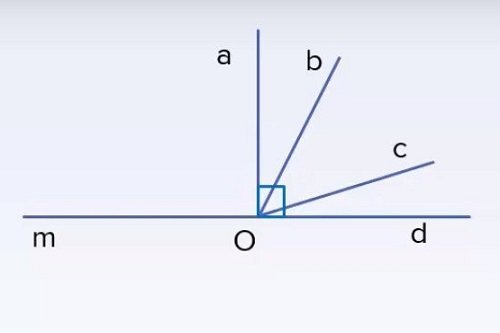
Bài tập 1: Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau:

Bài giải: Hai góc phụ nhau là hai góc có tổng số đo bằng 90. Vì vậy, trong hình vẽ có các cặp góc nhụ nhau là: góc aOb và góc bOd , góc cOd và cOa .

Hai góc bù nhau là hai góc có tổng số đo bằng 180. Vì vậy, trong hình vẽ có các cặp góc bù nhau là: góc dOc và góc cOm ,góc mOa và aOd .

Xem thêm : Nghị luận về nhận thức và trách nhiệm của tuổi trẻ trước hiện tượng lãng phí – Văn mẫu 10 hay nhất

Bài tập 2: Cho hình vẽ bên dưới. Tìm cặp góc phụ nhau?

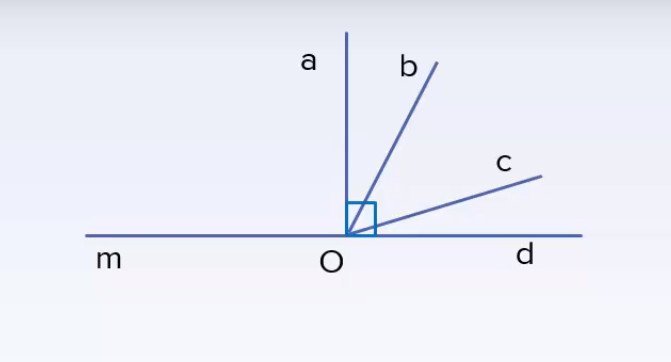
Ta có góc uOy = 90.

Tia Oz nằm giữa hai tia Ou và Oy

Suy ra góc yOz + zOu = 90.

Vậy góc yOz kề và phụ với góc zOu.

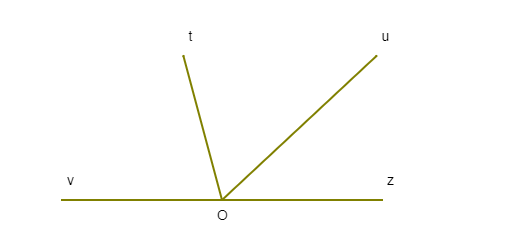
Bài tập 3: Cho biết hai góc kề bù góc tOu và góc uOv (như hình vẽ bên dưới), biết góc tOu= 36. Tính góc uOv ?

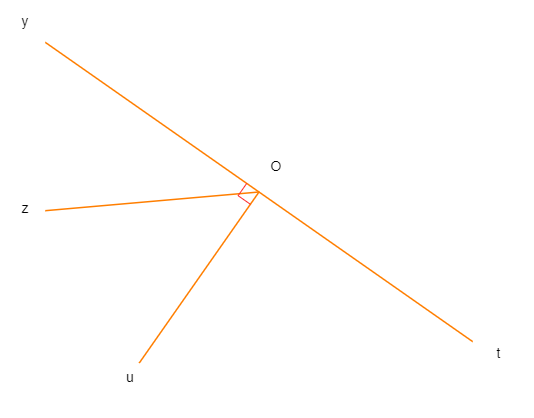
Vì hai góc tOu và góc uOv kề bù nên góc tOu + uOv = 180.

Suy ra: góc uOv = 180 – tOu = 180 – 36 = 144.

Bài tập 4: Cho hình vẽ bên dưới. Tìm góc kề bù với góc uOv ?

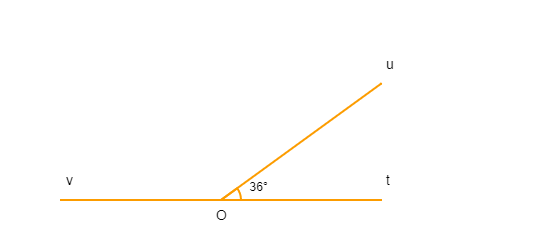
Do góc uOv + zOu = zOv = 180.

Nên góc zOu (hoặc tên gọi khác uOz ) là góc kề bù với uOv.

Bài tập 5:

Xem hình bs.5

a) Gọi tên cặp góc kề nhau đỉnh O xuất hiệ trong hình.

b) Cho biết các cặp góc phụ nhau đỉnh O.

c) Cho biết các cặp góc bù nhau đỉnh O.

d) Cho biết các cặp góc kề bù nhau đỉnh O

Bài giải:

Xem thêm : Học lực khá nên chọn ngành nào khối D?

a) Chúng ta có cặp góc kề nhau đỉnh O: mOn và nOw; mOn và nOz; mOn và nOt; mOw và zOw; mOw và tOw; mOz và zOt; wOn và zOw; wOn và tOw; wOz và zOt.

b) mOn và nOw ; wOz và zOt

c) mOn và nOt ; wOm và wOt ; mOz và zOt.

d) mOn và nOt ; wOm và wOt ; mOz và zOt.

Bài tập 6:

Chỉ ra câu đúng và câu sai.

a) Hai góc có tổng bằng 180° là hai góc kề bù.

b) Hai góc kề bù nếu tia đối góc này là tia đối của góc kia.

c) Hai góc nhọn đó là hai góc phụ nhau.

d) Hai góc nhọn đó là hai góc bù nhau.

e) Hai góc vuông đó là hai góc kề bù.

f) Hai góc phụ nhau trong khi góc này là 45° thì góc kia sẽ là 135°.

g) Hai góc bù nhau thì một góc là 45° thì góc kia sẽ là 45°.

Bài giải:

Tất cả các câu trên đều sai. Không có câu nào đúng.

Vấn đề mở rộng của 2 góc phụ nhau

Khi hai góc xOy và góc zOt phụ nhau thì ta có:

sin (xOy)=cos (zOt)

sin (zOt)=cos (xOy)

tan (xOy)=cot (zOt)

tan (zOt)=cot (xOy)

Nói một cách dễ hiểu là nếu hai góc phụ nhau thì Sin góc này bằng Cos góc kia, Tan góc này bằng Cot góc kia.

Xem thêm: Các công thức toán học 12

Qua bài viết này, hi vọng các bạn sẽ hiểu được thế nào là hai góc kề nhau, 2 góc bù nhau, 2 góc phụ nhau, phân biệt được sự khác nhau giữa góc phụ nhau với góc bù nhau và giải được một số bài tập có liên quan đến tính chất hai góc phụ, không có gì quá khó hiểu phải không nào các bạn. Các bạn hãy giải lại các bài tập để có thể nắm vững được kiến thức hơn. Nếu có gì thắc mắc không hiểu, các bạn hãy comment dưới bài viết này, chúng tôi sẽ giải đáp cho các bạn trong thời gian sớm nhất có thể. Hãy theo dõi các bài viết tiếp theo trong loạt bài hướng dẫn về Toán học để có thể học tiến bộ hơn. Chúc các bạn học thành công!.

Bài Liên Quan:

Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu