Cách tính tọa độ trọng tâm tam giác cùng các dạng toán liên quan
- Phân phối chương trình Ngữ Văn 9
- Hãy đánh dấu (V) vào ô trước bệnh mà gả thường mắc phải. | SBT công nghệ 7 chân trời
- Toán Sử Anh là khối gì? Xét tuyển được những ngành nào? Học trường nào?
- Hợp kim chứa nguyên tố X nhẹ và bền, dùng chế tạo vỏ máy bay, tên lửa. Nguyên tố X còn được sử dụng trong xây dựng, ngành điện và đồ gia dụng. Nguyên tử của nguyên tố X có tổng số hạt (proton, electron, neutron) là 40. Tổng số hạt mang điện nhiều hơn tổng | SBT Hoá học 10 Kết nối tri thức
- Tên cúng cơm là gì? 101 tên cúng cơm cho bé trai, bé gái hay nhất
Cách tính tọa độ trọng tâm tam giác cùng các dạng toán liên quan
Tọa độ trọng tâm của tam giác cũng như cách tính tọa độ trọng tâm tam giác học sinh đã đươc tìm hiểu trong môn Hình học 10. Nhằm giúp các em nắm vững hơn phần kiến thức vô cùng quan trọng này, thcs Hồng Thái đã chia sẻ bài viết sau đây. Bạn tìm hiểu nhé !
Bạn đang xem: Cách tính tọa độ trọng tâm tam giác cùng các dạng toán liên quan
I. CÁCH TÍNH TỌA ĐỘ TRỌNG TÂM TAM GIÁC
1. Phương pháp giải
Bạn đang xem: Cách tính tọa độ trọng tâm tam giác cùng các dạng toán liên quan

Cho tam giác ABC có A(xA; yA), B(xB; yB), C(xC; yC). Nếu G là trọng tâm của tam giác ABC thì:

2. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M(2; 0) , N(2; 2), P(-1; 3) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tọa độ điểm B là:
A. B(1; 1)
B. B(1; -1)
C. B(-1;1)
D. B(-1; -1)
Hướng dẫn giải:

Gọi tọa độ của A(xA; yA), B(xB; yB), C(xC; yC)
M là trung điểm của BC nên ta có:  (1)
(1)
N là trung điểm của AC nên ta có:  (2)
(2)
P là trung điểm của AB nên ta có:  (3)
(3)
Từ (1), (2) và (3), cộng vế theo vế ta được: 

Gọi G là trọng tâm tam giác ABC
Suy ra tọa độ G: 
Ta có: 
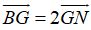
Suy ra:  B(-1; 1)
B(-1; 1)
Đáp án C
II. BÀI TẬP TÍNH TỌA ĐỘ TRỌNG TÂM TAM GIÁC
Bài 1: Trong mặt phẳng tọa độ Oxy, cho các điểm A(2; 0), B(0; 4), C(1; 3).
a, Chứng minh rằng A, B, C là 3 đỉnh của một tam giác.
b, Tìm tọa độ trong tâm tam giác ABC.
Hướng dẫn giải:
Xem thêm : Mệnh Giản Hạ Thủy nghĩa là gì? Sinh năm bao nhiêu?
a, Ta có: 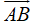
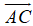
Do ![]() không cùng phương, suy ra A, B, C không thẳng hàng.
không cùng phương, suy ra A, B, C không thẳng hàng.
Vậy A, B, C là 3 đỉnh của một tam giác.
b, Gọi G là trọng tâm tam giác ABC. Suy ra tọa độ của G là:

Vậy tọa độ trọng tâm tam giác ABC là G (1; 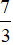
Bài 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; -1), B(5; -3) và C thuộc trục Oy, trọng tâm G của tam giác ABC nằm trên trục Ox. Tọa độ của điểm C là:
A. C(0; 4)
B. C(0; 2)
C. C(2; 0)
D. C(2; 4)
Hướng dẫn giải:
Ta có: 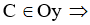
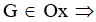
G là trọng tâm của tam giác ABC nên ta có:


Vậy C(0; 4).
Đáp án A
Bài 3: Tam giác ABC có C(-2; -4), trọng tâm G(0; 4), trung điểm BC là M(2; 0). Tọa độ của đỉnh A và đỉnh B là:
A. A(4; 12), B(4; 6)
B. A(-4; -12), B(6; 4)
C. A(-4; 12), B(6; 4)
D. A(4; -12), B(-6; 4)
Hướng dẫn giải:

Vì M là trung điểm BC nên

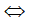
Vì G là trọng tâm tam giác ABC nên 
 A (-4; 12)
A (-4; 12)
Đáp án C
Bài 4: Trong mặt phẳng tọa độ Oxy, cho tam giác DEF với tọa độ ba điểm D(-4;1), E(2; 4) và F(2; -2).
a, Tìm tọa độ trọng tâm H của tam giác DEF.
b, Tìm tọa độ điểm K sao cho F là trọng tâm tam giác DEK.
Hướng dẫn giải:
a, Tọa độ trọng tâm H của tam giác DEF là
 H (0; 1)
H (0; 1)
b, Gọi tọa độ K(xK; yK)
Vì F là trọng tâm tam giác DEK nên ta có:


Thay số ta được: K (8; -11)
K (8; -11)
Bài 5:
Trong hệ tọa độ Oxy cho tam giác ABC có A(3 ; 5) ; B( 1 ;2) và C( 5 ;2). Tìm tọa độ trọng tâm G của tam giác ABC ?
a. G (-9;-9)
b. G (9/2;9/2)
c. G (3;3)
d. g (9;9)
Chọn C.
Ta có 
Bài 6: Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
a. D (-2;5)
b. D ( 12;5)
C. D (8;5)
D. D (8;-5)
Trả lời:
Chọn A.
Gọi tọa độ của D(x;y)
Khi đó AD⇀x+2;y; BC→-10;5
Ta có: tứ giác ABCD là hình bình hành khi BC→=AD→
x+2=-10y=5⇔x=-12y=5
Vậy tọa độ của D là: D(-12;5)
Vậy là các bạn vừa được tìm hiểu cách tính tọa độ trọng tâm tam giác và nhiều kiến thức liên quan khác trong chuyên đề này. Hi vọng, chia sẻ cùng bài viết, bạn đã nắm vững hơn phần kiến thức Hình học 10 quan trọng này. Xem thêm cách tính toạ độ trung điểm của đoạn thẳng tại đường link này nhé !
Đăng bởi: thcs Hồng Thái
Chuyên mục: Giáo dục
Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)
Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu