Chuyên đề Ước và Bội: Cách tìm ước chung và bội chung
Chuyên đề Ước và Bội: Cách tìm ước chung và bội chung học sinh đã được tìm hiểu trong chương trình Toán 6. Phần kiến thức này rất quan trọng trong chương trình và xuất hiện nhiều trong các đề thi. Để giúp các em nắm vững hơn các kiến thức cần ghi nhớ, thcs Hồng Thái đã chia sẻ bài viết sau đây.
Bạn đang xem: Chuyên đề Ước và Bội: Cách tìm ước chung và bội chung
I. KIẾN THỨC CHUNG
1. Khái niệm Ước và Bội
Bạn đang xem: Chuyên đề Ước và Bội: Cách tìm ước chung và bội chung
Nếu số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b và b là ước của a.
Tập hợp các bội của a được kí hiệu bởi B(a).
Tập hợp các ước của a được kí hiệu bởi Ư(a).
Ví dụ: 35 chia hết cho 5 nên 35 là bội của 5 và 5 là ước của 35
2. Cách tìm ước chung lớn nhất, bội chung nhỏ nhất
* Bổ sung:
+ Tích của hai số tự nhiên khác 0 bằng tích của ƯCLN và BCNN của chúng:
a . b = ƯCLN(a,b). BCNN(a,b)
+ Nếu tích a.b chia hết cho m, trong đó b và m là hai số nguyên tố cùng nhau thì a m
+ Một cách khác tìm ƯCLN của hai số a và b (với a > b):
Chia số lớn cho số nhỏ.
Nếu a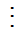 
b thì ƯCLN(a,b) = b
– Nếu phép chia a cho b có số dư r1, lấy b chia cho r1.
– Nếu phép chia b cho r1 có số dư r2, lấy r1 chia cho r2.
– Cứ tiếp tục như vậy cho đến khi số dư bằng 0 thì số chia cuối cùng là ƯCLN phải tìm.
3. Cách kiểm tra 1 số là số nguyên tố
Để kết luận số a là số nguyên tố (a > 1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.
– Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố
4. Cách tính số lượng các ước của một số m (m > 1)
Ta xét dạng phân tích của số m ra thừa số nguyên tố: Nếu m = ax thì m có x + 1 ước
Nếu m = ax. by thì m có (x + 1)(y + 1) ước
Nếu m = ax. by. cz thì m có (x + 1)(y + 1)(z + 1) ước.
– Ước chung của hai hay nhiều số là ước của tất cả các số đó.
– Bội chung của hai hay nhiều số là bội của tất cả các số đó.
– ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
– Các số nguyên tố cùng nhau là các số có ƯCLN bằng 1
– Để tìm ước chung của các số đã cho, ta có thể tìm các ước của ƯCLN của các số đó.
– BCNN của hai hay nhiều số là số lớn nhất khác 0 trong tập hợp các bội chung của các số đó.
– Để tìm BC của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.
5. Các dạng toán cơ bản
Dạng 1: Tìm và viết tập hợp các ước, tập hợp các bội của một số cho trước
Phương pháp:
– Để tìm ước của một số, ta chia số đó lần lượt cho 1, 2, 3…
– Để tìm bội của một số khác 0, ta nhân số đó lần lượt với 0, 1, 2, 3…
Ví dụ: Ư(18)={18;9;6;3;2;1}
B(5)={0;5;10;15;…}
Dạng 2: Viết tất cả các số là bội hoặc ước của một số cho trước và thỏa mãn điều kiện cho trước
Phương pháp:
Tìm trong các số thỏa mãn điều kiện cho trước những số là bội hoặc ước của số đã cho.
Ví dụ: Tìm các ước lớn hơn 5 của 20.
Ta có: Ư(20)={20;10;5;4;2;1}
Suy ra các ước lớn hơn 5 của 20 là 20 và 10.
II. BÀI TẬP VẬN DỤNG
Bài 1. Viết tập hợp các bội chung của 4 và 6
Bài 2. Tìm ước chung của a và a + 1
Bài 3. Tìm tập hợp các ước chung của 51 và 76
Bài 4. Tìm các ước chung của 2n và 2n + 2
Bài 5. Số1080 chia hết cho những số nào sau đây: 2, 3, 4, 5, 6, 8, 9, 12, 25?
Bài 6. Tìm số tự nhiên x, biết rằng 30 chia hết cho x có dư là 6 và 45 chia cho x có dư là 9.
Bài 7. Viết các tập hợp: B(2); B(5) và BC(2, 5)
Bài 8. Tìm các ước chung của 6x+5 và 6x (x∈N)
Bài 9. Có 15000 đồng có thể mua hai loại vở 2000 đồng và 5000 đồng (một cuốn). Hỏi có thể mua được bao nhiêu vở mỗi loại (mua cả 2 loại và mua hết số tiền đã mang theo).
Bài 10. Tìm các ước chung có ba chữ số của 5, 6 và 9
Bài 11. Tìm các ước chung của 4n+3 và 2n; n∈N
Bài 12. Tìm số tự nhiên x, nhỏ hơn 400; biết rằng x chia cho 4, cho 5, cho 6 đều có dư là 1 và x chia hết cho 7.
Bài 13. Số n chia hết cho 3 có dư là 1, chia cho 2 có dư là 2. Tìm tập hợp các số n
Bài 14. Viết tập hợp các ước chung của n; n+1 và n+2, n∈N
Lời giải chi tiết
Bài 1. B(4)={0,4,8,12,16,…}
B(6)={0,6,12,1,8,…}
⇒BC(4;6)={0,12,24,…}
Bài 2. Gọi d là một ước chung của a và a + 1
a⋮d và a+1⋮d ⇒(a+1–a)⋮d
⇒1⋮d⇒d=1
Bài 3. Ư(51)={1,3,17,51}.
Ư(76)={1,2,4,19,76}
⇒ƯC(51;76)={1}
Bài 4. Gọi d là một ước chung của 2n và 2n+2⇒2n⋮d, (2n+2)⋮d
⇒(2n+2−2n)⋮d⇒2⋮d
Vậy d=1 hoặc d=2
Bài 5. Ta có: 1080 chia hết cho 2, 3, 4, 5, 6, 8, 9 ,15, không chia hết cho 25.
Bài 6. Vì 30 chia cho x có dư là 6 nên 30–6=24 chia hết cho x,
Tương tự: 45–9=36 chia hết cho x
Vậy x là ước chung của 24 và 36 (với x>9)
Xem thêm : Trọng tâm là gì? Khái niệm, tính chất và cách xác định
Ta có: Ư(24)={1,2,3,4,6,12,24}
Ư(36)={1,2,3,4,6,9,12,8,36}
⇒ƯC(24,36)={1,2,3,4,6,12}
Vì x>9⇒x=12
Bài 7. B(2)={0,2,4,6,…}
B(5)={0,5,10,15,…}
⇒BC(2,5)={0,10,20,…}
Bài 8. Gọi y là ước chung của 6x+5 và 6x
⇒(6x+5)⋮y, 6x⋮y ⇒(6x+5–6x)⋮y ⇒5⋮y
Vậy Ư(5)={1,5}⇒y∈{1,5}
Bài 9.
Ta có:
B(2000)={0,2000,4000,…}
B(5000)={0,5000,1000,…}
Vì 15000=5000+10000=5000.1+2000.5
Nên ta chọn mua 2 cuốn vở 5000 đồng và 5 cuốn vở 2000 đồng.
Bài 10. B(5)={0,5,10,…}
B(6)={0,6,12,18,…}
B(9)={0,9,18,…}
Vậy BC(5,6,9)={0,90,180,270,…}
Các bội có ba chữ số: 180, 270, 360, 450, 540, 630, 720, 810, 900, 990,
Bài 11. Gọi d là một ước chung của 4n+3và 2n
⇒(4n+3)⋮d và 2n⋮d ⇒(4n+3)⋮d và 2.(2n)⋮d
⇒(4n+3–4n)⋮d⇒3⋮d ⇒d∈{1,3}
Bài 12. Vì x chia cho 4, cho 5 và cho 6 đều dư là 1 nên:
(x–1)⋮4;(x–1)⋮5;(x–1)⋮6
BC(4,5,6)={0,60,120,180,240,…}
Vì x
Bài 13. x chia cho 3 và 2 đều dư 1 ⇒(x–1)⋮2 và (n–1)⋮3.
Mà BC(2,3)={0,6,12,18,…}
Vậy n−1=6k,k∈N ⇒ n=6k+1,k∈N
Bài 14. Ta có:
ƯC(n,n+1)={1}
Khi đó: ƯC(1,n+2)={1}
Vậy ƯC(1,n+1,n+2)={1} với n∈N
Vậy là các bạn vừa được tìm hiểu chuyên đề Ước và Bội: Cách tìm ước chung và bội chung một cách nhanh nhất. Trong những bài viết tiếp theo thcs Hồng Thái sẽ tiếp tục giới thiệu kĩ hơn cách tìm ước chung lớn nhất, bội chung nhỏ nhất để các bạn nắm rõ chắc bài hơn. Bạn nhớ đón xem nhé ! Và đừng quên tìm hiểu thêm các tính chất của phép nhân và phép cộng nữa nhé !
Đăng bởi: thcs Hồng Thái
Chuyên mục: Giáo dục
Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)
Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu
