7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán

5 10 minutes read

Có thể bạn quan tâm

3 Đề đọc hiểu khoảng trời hố bom của Lâm Thị Mỹ Dạ hay nhất
Một người tập luyện chạy bộ xuất phát lúc 5 giờ 05 phút 01 giây theo hướng từ nhà đến cột đèn và tới chân cột đèn lúc 5 giờ 09 phút 05 giây. Ngay sau đó, từ cột đèn người này chạy theo hướng ngược lại và chạy ngang qua cây bàng bên vệ đường lúc 5 giờ 19 p
Giải SBT bài 2 Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác | SBT Toán 7 Cánh diều
Phân tích tác phẩm Chí Phèo của Nam Cao
Mỹ Tâm là ai? Tiểu sử, sự nghiệp, đời tư, tình cảm của nữ ca sĩ

7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán

7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán học sinh đã được tìm hiểu trong chường trình Toán 8, phân môn Đại số. Phần kiến thức này khá quan trọng trong chương trình, liên quan đến nhiều dạng toán giải phương trình khác nữa. Để nắm rõ hơn các kiến thức cần ghi nhớ, hãy chia sẻ bài viết sau đây bạn nhé !

Bạn đang xem: 7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán

I. LÝ THUYẾT VỀ 7 HẰNG ĐẲNG THỨC ĐÁNG NHỚ

1. Bảy hằng đẳng thức đáng nhớ là gì ?

Bạn đang xem: 7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán

Bảy hằng đẳng thức đáng nhớ là những đẳng thức cơ bản nhất mà mỗi người học toán cần phải nắm vững. Các đẳng thức được chứng minh bằng phép nhân đa thức với đa thức.Các hàng đẳng thức này nằm trong nhóm các hàng đẳng thức đại số cơ bản, bên cạnh nhiều hàng đẳng thức khác.

Những đẳng thức này được sử dụng thường xuyên trong các bài toán liên quan đến giải phương trình, nhân chia các đa thức, biến đổi biểu thức tại cấp học THCS và THPT. Học thuộc bảy hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán phân tích đa thức thành nhân tử.

2. Bảy hằng đẳng thức đáng nhớ và hệ quả

a. Bảy hằng đẳng thức đáng nhớ:

Bình phương của một tổng:

${displaystyle (a+b)^{2}=a^{2}+2ab+b^{2},}$

$Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai$
Bình phương của một hiệu:

${displaystyle (a-b)^{2}=a^{2}-2ab+b^{2},}$

$Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.$
Hiệu hai bình phương:

${displaystyle a^{2}-b^{2}=(a-b)(a+b),}$

$Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.$
Lập phương của một tổng:

${displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3},}$

$Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.$
Lập phương của một hiệu:

${displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3},}$

$Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai$
Tổng hai lập phương:

${displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2}),}$

$Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó$
Hiệu hai lập phương:

${displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2}),}$

$Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.$

b. Hệ quả hằng đẳng thức

Ngoài ra, ta có các hằng đẳng thức hệ quả của 7 hằng đẳng thức trên. Thường sử dụng trong khi biến đổi lượng giác chứng minh đẳng thức, bất đẳng thức,…

Hệ quả với hằng đẳng thức bậc 2

$(a+b)^2=(a-b)^2+4ab$

$(a-b)^2=(a+b)^2-4ab$

$a^2+b^2=(a+b)^2-2ab$

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$(a+b-c)^2=a^2+b^2+c^2+2ab-2ac-2bc$

$(a-b-c)^2=a^2+b^2+c^2-2ab-2ac-2bc$

Hệ quả với hằng đẳng thức bậc 3

$a^3+b^3=(a+b)^3 - 3ab(a+b)$

$a^3-b^3=(a-b)^3 + 3ab(a-b)$

$(a+b+c)^3=a^3+b^3+c^3+3(a+b)(a+c)(b+c)$

$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$

$(a-b)^3+(b-c)^3+(c-a)^3=3(a-b)(b-c)(c-a)$

$(a+b)(b+c)(c+a)-8abc=a(b-c)^2+b(c-a)^2+c(a-b)^2$

$(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)-abc$

$(a+b)(b+c)(c+a)-8abc=a(b-c)^2+b(c-a)^2+c(a-b)^2$

$(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)-abc$

Hệ quả tổng quát

$a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-a^{n-4}b^3+ldots+a^2b^{n-3}-acdot b^{n-2}+b^{n-1})$

$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+ldots+a^2b^{n-3}+ab^{n-2}+b^{n-1})$

3. Một số lưu ý về hằng đẳng thức đáng nhớ

+ Biến đổi các hằng đẳng thức chủ yếu là cách biến đổi từ tổng, hiệu thành tích giữa các số, kỹ năng phân tích đa thức thành nhân tử phải thành thạo thì áp dụng các hằng đẳng thức mới rõ ràng và chính xác được.

+ Để hiểu rõ về bản chất sử dụng hằng đẳng, khi áp dụng vào bài toán, học sinh có thể chứng minh sự tồn tại của hằng đẳng thức là đúng đắn bằng cách chuyển đổi ngược lại, sử dụng các hằng đẳng liên quan vào việc chứng minh bài toán.

+ Trong khi sử dụng hằng đẳng thức trong phân thức đại số, học sinh cần lưu ý rằng sẽ có nhiều hình thức biến dạng của công thức do tính chất mỗi bài toán nhưng bản chất vẫn là những công thức ở trên, chỉ là sự biến đổi qua lại để phù hợp trong việc tính toán.

Ví dụ :

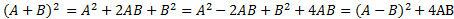
Lưu ý về 7 hằng đẳng thức đáng nhớ

4. Mẹo ghi nhớ nhanh các hằng đẳng thức

Nếu để ý, ta có thể nhận thấy rằng, các hằng đẳng thức số 1 và 2, 4 và 5, 6 và 7 đều khá tương tự nhau, chỉ khác nhau ở dấu, vì vậy điều cần lưu ý ở đây chính là ghi nhớ dấu của chúng, từ đó ta có thể học thuộc một cách chính xác và không bị nhầm lẫn.

Đối với hằng đẳng thức số 5 và 6 thì cần lưu ý đó chính là:

“Tổng các lập phương bằng tích của tổng hai số và bình phương thiếu của một hiệu”

“ Hiệu các lập phương bằng tích của hiệu hai số và bình phương thiếu của một tổng”

Ngoài ra các bạn có thể sưu tầm thêm bài hát về “7 Hằng Đẳng Thức Đáng Nhớ” do tác giả “Nhật Anh sáng tạo” dựa trên nhạc của bài hát “Sau Tất Cả”. Chắc chắn rằng, khi nghe bài hát này, các bạn học sinh có thể vừa thư giãn, vừa có thể ghi nhớ kiến thức một cách tự nhiên nhất mà không cảm thấy khô khan khó hiểu.

Tuy nhiên, tất cả cũng chỉ góp phần nhỏ bé thôi, quan trọng nhất bạn cần nắm rõ bản chất của nó và không ngừng rèn luyện, luyện tập và làm bài tập chăm chỉ bạn sẽ dẽ dàng ghi nhớ thôi.

II. CÁC DẠNG TOÁN THƯỜNG GẶP

Dạng 1: Tìm giá trị nhỏ nhất của biểu thức
Ví dụ: Tính giá trị nhỏ nhất của biểu thức: A = x² – 2x + 5
* Lời giải:
– Ta có : A = x² – 2x + 5 = (x² – 2x + 1) + 4 = (x – 1)²+ 4
– Vì (x – 1)²≥ 0 với mọi x.
⇒ (x – 1)²+ 4 ≥ 4 hay A ≥ 4
– Vậy giá trị nhỏ nhất của A = 4, Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
⇒ Kết luận GTNN của A là: A_min= 4 ⇔ x = 1
Dạng 2 : Tìm giá trị lớn nhất của biểu thức
Ví dụ: Tính giá trị lớn nhất của biểu thức: A = 4x – x²
* Lời giải:
– Ta có : A = 4x – x²= 4 – 4 + 4x – x²= 4 – (4– 4x + x²) = 4 – (x²– 4x + 4) = 4 – (x – 2)²
– Vì (x – 2)²≥ 0 với mọi x ⇔ -(x – 2)² ≤ 0 với mọi x
⇔ 4 – (x – 2)²≤ 4 [cộng 2 vế với 4]⇔ A ≤ 4 Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
⇒ Kết luận GTLN của A là: A_max= 4 ⇔ x = 2.

Dạng 3 : Tính giá trị của biểu thức
Ví dụ: Tính giá trị của biểu thức : A = x² – 4x + 4 tại x = -1
* Lời giải.
– Ta có : A = x² – 4x + 4 = x² – 2.x.2 + 2² = (x – 2)²
– Tại x = -1 : A = ((-1) – 2)²=(-3)²= 9
⇒ Kết luận: Vậy tại x = -1 thì A = 9
Dạng 4 : Chứng minh biểu thức A không phụ thuộc vào biến
Ví dụ: Chứng minh biểu thức sau không phụ thuộc vào x: A = (x – 1)² + (x + 1)(3 – x)
* Lời giải.
– Ta có: A =(x – 1)² + (x + 1)(3 – x) = x² – 2x + 1 – x² + 3x + 3 – x = 4 : hằng số không phụ thuộc vào biến x.

Dạng 5 : Chứng minh đẳng thức bằng nhau
Ví dụ: Chứng minh đẳng thức sau đúng: (a + b)³ – (a – b)³ = 2b(3a² + b²)
* Lời giải:
– Đối với dạng toán này chúng ta biến đổi VT = VP hoặc VT = A và VP = A
– Ta có: VT = (a + b)³ – (a – b)³
= (a³ + 3a²b + 3ab² + b³) – (a³ – 3a²b + 3ab² – b³)
= a³ + 3a²b + 3ab² + b³ – a³ + 3a²b – 3ab² + b³
= 6a²b + 2b³
= 2b(3a² + b²) = VP (đpcm).
⇒ Kết luận, vậy : (a + b)³ – (a – b)³ = 2b(3a² + b²)
• Dạng 6 : Chứng minh bất đẳng thức
– Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Ví dụ: Chứng minh biểu thức B nhận giá trị âm với mọi giá trị của biến x, biết: B = (2-x)(x-4)-2
* Lời giải:
– Ta có: B = (2-x)(x-4) – 1 = 2x – 8 – x² + 4x – 2 = -x² + 6x – 9 – 1 = -(x² – 6x + 9) – 1 = -(x-3)² – 1
– Vì (x-3)² ≥ 0 ⇔ -(x-3)² ≤ 0 ⇒ -(x-3)² – 1 ≤ -1 < 0 với mọi x,

Xem thêm : Sơ đồ tư duy Chữ người tử tù – Nguyễn Tuân

Dạng 7: Tìm giá trị của x
Ví dụ:Tìm giá trị củ x biết: x²( x – 3) – 4x + 12 = 0
* Lời giải.
x² (x – 3) – 4x + 12 = 0
⇔ x² (x – 3) – 4(x – 3) = 0
⇔ (x – 3) (x² – 4) = 0
⇔ (x – 3)(x – 2)(x + 2) = 0
⇔ (x – 3) = 0 hoặc (x – 2) = 0 hoặc (x + 2) = 0
⇔ x = 3 hoặc x = 2 hoặc x = –2
⇒ Kết luận, vậy nghiệm : x = 3; x = 2; x = –2

Dạng 7: Phân tích đa thức thành nhân tử

Ví dụ:Phân tích đa thức sau thành nhân tử: A = x² – 4x + 4 – y²
* Lời giải:
– Ta có : A = x² – 4x + 4 – y² [để ý x² – 4x + 4 có dạng hằng đẳng thức]= (x² – 4x + 4) – y² [nhóm hạng tử]= (x – 2)²– y² [xuất hiện đẳng thức số A² – B²]= (x – 2 – y )( x – 2 + y)
⇒ A = (x – 2 – y )( x – 2 + y)

III. BÀI TẬP VỀ HẰNG ĐẲNG THỨC

Bài 1: Tính nhanh

$1. 1001^{2}$

2. 29,9.30,1

$3. 201^{2}$

4. 37.43

$5. 199^{2}$

$6. 37^{2}+2.37 .13+13^{2} \$

$7. 51,7-2.51,7.31,7+31,7^{2} \$

$8. 20,1.19,9 \$

$9. 31,8^{2}-2.31,8.21,8+21,8^{2} \$

$10.33,3^{2}-2.33,3.3,3+3,3^{2}\$

Bài 2: Rút gọn rồi tính giá trị biểu thức

$1. (mathrm{x}-10)^{2}-mathrm{x}(mathrm{x}+80)$

$2. (2 mathrm{x}+9)^{2}-mathrm{x}(4 mathrm{x}+31)$

$3. 4 mathrm{x}^{2}-28 mathrm{x}+49$

$4. mathrm{x}^{3}-9 mathrm{x}^{2}+27 mathrm{x}-27$

Bài 3 : Chứng minh với moi số nguyên N biểu thức $(2 n+3)^{2}-9$ chia hết cho 4

Bài 4 : Viết biểu thức sau dưới dang tích

$a. (x+y+x)^{2}-2(x+y+x)(y+z)+(y+z)^{2}$

$b. (x+y+x)^{2}-(y+z)^{2}$

$c. (x+3)^{2}+4(x+3)+4$

$d. 25+10(x+1)+(x+1)^{2}$

Bài 5. Viết biểu thức sau dưới dang tích

$a. x^{2}-2$

$b. y^{2}-13$

$c. 2 x^{2}-4$

$d. left(x^{2}-1right)^{2}-(y+3)^{2}$

$e. left(a^{2}-b^{2}right)^{2}-left(a^{2}+b^{2}right)^{2}$

Bài 6. Viết biểu thức sau dưới dang tích

$a. -4 x^{2}+9 y^{2}$

$b .8+(4 x-3)^{3}$

Bài 7. Viết biểu thức sau dưới dạng tổng

$a. (x+y+z+t) cdot(x+y-z-t)$

b.. $(x+2 y+3 z+t)^{3}.$

Bài 8: Viết biểu thức sau dưới dạng tổng

$a. left(x^{2}-2 x-1right)^{2}$

b. $left(m^{2}+2 m-3right)^{2}.$

$text { c. }(x+1)left(x^{2}+1right)left(x^{4}+1right)$

$d.2. (3+1)left(3^{2}+1right)left(3^{4}+1right)$

****Các bài toán nâng cao về hằng đẳng thức (có đáp án)

Bài 1. Cho đa thức 2x² – 5x + 3 . Viết đa thức trên dưới dạng 1 đa thức của biến y trong đó y = x + 1.

Lời Giải

Theo đề bài ta có: y = x + 1 => x = y – 1.

A = 2x² – 5x + 3

= 2(y – 1)² – 5(y – 1) + 3 = 2(y² – 2y + 1) – 5y + 5 + 3 = 2y² – 9y + 10

Bài 2. Tính nhanh kết quả các biểu thức sau:

Xem thêm : Lý thuyết hình bình hành. Cách chứng minh tứ giác là hình bình hành cực hay

a) 127² + 146.127 + 73²

b) 9⁸.2⁸– (18⁴ – 1)(18⁴ + 1)

c) 100² – 99² + 98² – 97² + …+ 2² – 1²

d) (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)

Lời Giải

a) A = 127² + 146.127 + 73²

= 127² + 2.73.127 + 73²

= (127 + 73)²

= 200²

= 40000 .

b) B = 9 ⁸.2 ⁸– (18 ⁴– 1)(18 ⁴+ 1)

= 18⁸ – (18⁸ – 1)

= 1

c) C = 100² – 99² + 98² – 97² + …+ 2² – 1²

= (100 + 99)(100 – 99) + (98 + 97)(98 – 97) +…+ (2 + 1)(2 – 1)

= 100 + 99 + 98 + 97 +…+ 2 + 1

= 5050.

d) D = (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)

= (20² – 19²) + (18² – 17²) + (16² – 15²)+ …+ (4² – 3²) + (2² – 1²)

= (20 + 19)(20 – 19) + (18 + 17)(18 – 17) + ( 16 +15)(16 – 15)+ …+ (4 + 3)(4 – 3) + (2 + 1)(2 – 1)

= 20 + 19 + 18 + 17 + 16 +15 + …+ 4 + 3 + 2 + 1

= 210

Bài 3. So sánh hai số sau, số nào lớn hơn?

a) A = (2 + 1)(2²+ 1)(2⁴+ 1)(2⁸ + 1)(2¹⁶ + 1) và B = 2³²

b) A = 1989.1991 và B = 1990²

Gợi ý đáp án

a) Ta nhân 2 vế của A với 2 – 1, ta được:

A = (2 – 1)(2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)

Ta áp dụng đẳng thức ( a- b)(a + b) = a² – b² nhiều lần, ta được:

A = 2³² – 1.

=> Vậy A < B.

b) Ta đặt 1990 = x => B = x²

Vậy A = (x – 1)(x + 1) = x² – 1

=> B > A là 1.

Bài 4. Chứng minh rằng:

a) a(a – 6) + 10 > 0.

b) (x – 3)(x – 5) + 4 > 0.

c) a² + a + 1 > 0.

Lời Giải

a) VT = a² – 6a + 10 = (a – 3)² + 1 ≥ 1

=> VT > 0

b) VT = x² – 8x + 19 = (x – 4)² + 3 ≥ 3

=> VT > 0

c) a² + a + 1 = a² + 2.a.½ + ¼ + ¾ = (a + ½ )² + ¾ ≥ ¾ >0.

Vậy là các bạn vừa được tìm hiểu 7 hằng đẳng thức đáng nhớ và hệ quả cùng các dạng toán thường gặp. Hi vọng, bài viết đã cung cấp cho bạn thêm nhiều thông tin hữu ích. Xem thêm chuyên đề về tỉ lệ thức tại đường link này nữa bạn nhé !

Đăng bởi: thcs Hồng Thái

Chuyên mục: Giáo dục

Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!

Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)

Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu

THCS Hồng Thái

5 10 minutes read