Cách viết phương trình đường trung trực của 1 đoạn thẳng – Toán 10 chuyên đề

- Từ phức là gì? Có mấy loại từ phức? Cách tạo ra từ phức? Phân biệt với từ ghép
- Số orbital trong các phân lớp s, p, d lần lượt bằng | SBT Hoá học 10 Kết nối tri thức
- Các dạng toán tìm số trung bình cộng: phương pháp giải & bài tập
- Phân tích bài thơ Đây thôn Vĩ Dạ của Hàn Mặc Tử lớp 11 hay nhất (25 Mẫu)
- One Swallow Doesn’t Signal the Arrival of Spring
Cùng thcs Hồng Thái tìm hiểu Cách viết phương trình đường trung trực của 1 đoạn thẳng – Toán 10 chuyên đề
Bạn đang xem: Cách viết phương trình đường trung trực của 1 đoạn thẳng – Toán 10 chuyên đề
Vậy cách viết phương trình đường trung trực của một đoạn thẳng như thế nào? chúng ta sẽ cùng tìm hiểu qua bài viết dưới đây và cùng xem các bài tập và ví dụ minh họa để hiểu rõ nhé.
Các em có thể xem lại nội dung phương trình tổng quát, phương trình tham số, phương trình chính tắc của đường thẳng nếu các em chưa nhớ rõ phần kiến thức này.
° Cách viết phương trình đường trung trực của một đoạn thẳng
Đường trung trực của đoạn thẳng AB chính là đường thẳng đi qua trung điểm I của đoạn thẳng này và nhận vectơ 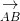 làm VTPT (như vậy dạng bài tập này tương trở về cách viết phương trình đường thẳng đi qua 1 điểm và có vectơ pháp tuyến n). Cụ thể
làm VTPT (như vậy dạng bài tập này tương trở về cách viết phương trình đường thẳng đi qua 1 điểm và có vectơ pháp tuyến n). Cụ thể
– Cho hai điểm A(xA; yA) và điểm B(xB; yB). Viết phương trình đường trung trực của đoạn thẳng AB:
+ Gọi (d) là đường trung trực của đoạn thẳng AB.
Khi đó (d) đi qua trung điểm M của AB và d vuông góc AB.
⇒ Phương trình đường thẳng (d) đi qua M và có VTPT 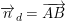
⇒ Phương trình đường thẳng d.
* Ví dụ 1: Viết phương trình đường thẳng (d) vuông góc với đường thẳng AB và đi qua trung điểm của AB biết: A(3;-1) và B(5;3).
* Lời giải:
– Vì (d) vuông góc với AB nên nhận 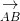 = (2;4) làm vectơ pháp tuyến
= (2;4) làm vectơ pháp tuyến
– Mặt khác (d) đi qua trung điểm I của AB, và I có toạ độ:
xi = (xA+xB)/2 = (3+5)/2 = 4;
yi = (yA+yB)/2 = (-1+3)/2 = 1;
⇒ toạ độ của I(4;1)
⇒ Vậy (d) đi qua I(4;1) có VTPT 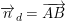 = (2;4) có PTTQ là:
= (2;4) có PTTQ là:
Xem thêm : Giải SBT bài 35: Thực hành: Cảm ứng ở sinh vật
2(x – 4) + 4(y – 1) = 0
⇔ 2x + 4y -12 = 0
⇔ x + 2y – 6 = 0.
* Ví dụ 2: Viết phương trình đường trung trực của đoạn AB biết A(-2; 3) và B(4; -1).
* Lời giải:
+ Gọi M là trung điểm của đoạn AB, khi đó, ta có:
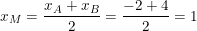
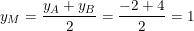
⇒ Tọa độ điểm M(1;1)
– Ta lại có: 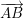 = (6; -4) = 2(3;-2)
= (6; -4) = 2(3;-2)
– Ta gọi (d) là đường thẳng trung trực của AB, khi đó:
(d) qua M( 1; 1) và nhận 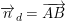 =(3;-2) làm VTPT.
=(3;-2) làm VTPT.
⇒ Phương trình (d) là: 3(x – 1) – 2(y – 1) = 0
Hay (d): 3x – 2y – 1 = 0
* Ví dụ 3: Viết phương trình đường trung trực của đoạn AB biết A(1;-4) và B(5;2).
* Lời giải:
– Gọi I là trung điểm của AB, khi đó tọa độ của điểm I là:
![]()
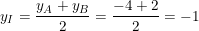
Xem thêm : Top 40+ ảnh bìa FB đẹp, Ảnh bìa Facebook chất nhất
⇒ Tọa độ điểm I(3;-1)
– Lại có: =(4;6)=2.(2;3)
– Gọi (d) là trung trực đoạn AB khi đó:
(d) qua I(3;-1) và nhận 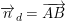 =(2;3) làm VTPT.
=(2;3) làm VTPT.
⇒ Phương trình (d) là: 2(x – 3) + 3(y + 1) = 0
Hay (d): 2x + 3y – 3 = 0
° Ngoài cách đã hướng dẫn ở trên, các em có thể dùng cách khác vận dụng công thức tính chiều dài.
– Gọi M(x; y) là điểm bất kỳ thuộc đường trung trực của đoạn thẳng AB. Khi đó, ta có: MA = MB.
Mặt khác, thì: MA2 = (xA – xM)2 + (yA – yM)2
MB2 = (xB – xM)2 + (yA – yM)2
Và từ MA = MB ta được kết quả.
Hy vọng với bài viết Cách viết phương trình đường trung trực của 1 đoạn thẳng ở trên hữu ích cho các em. Mọi thắc mắc các em vui lòng để lại bình luận dưới bài viết để thcs Hồng Thái ghi nhận và hỗ trợ. Chúc các em học tập tốt!
Đăng bởi: thcs Hồng Thái
Chuyên mục: Giáo Dục
Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)
Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu

