Cách tính đạo hàm của hàm căn thức và các dạng toán thường gặp

Cách tính đạo hàm của hàm căn thức và các dạng toán thường gặp

Bài viết hôm trước thcs Hồng Thái đã giới thiệu đến quý thầy cô và các bạn công thức tính nhanh đạo hàm của các hàm số thường gặp. Tiếp tục mạch kiến thức đó, hôm nay chúng tôi sẽ giới thiệu cách tính đạo hàm của hàm căn thức và các dạng toán thường gặp. Bạn hãy chia sẻ để tìm hiểu nhé !

Bạn đang xem: Cách tính đạo hàm của hàm căn thức và các dạng toán thường gặp

I. ĐẠO HÀM LÀ GÌ ?

Trong giải tích toán học, đạo hàm của một hàm số thực chất là sự mô tả sự biến thiên của hàm số tại một điểm nào đó. 

Bạn đang xem: Cách tính đạo hàm của hàm căn thức và các dạng toán thường gặp

Trong vật lý, đạo hàm biểu diễn vận tốc tức thời của một điểm chuyển động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn.

Trong hình học đạo hàm là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Tiếp tuyến đó là xấp xỉ tuyến tính gần đúng nhất của hàm ở gần giá trị đầu vào.

II. CÁCH TÍNH ĐẠO HÀM CỦA HÀM CĂN THỨC

Để tính đạo hàm của hàm căn thức hay hàm chứa căn thức ta áp dụng công thức sau đây:

Ví dụ minh họa

Xem thêm : Công thức tính tích có hướng của hai vectơ trong không gian và bài tập

Bài số 1: Tính đạo hàm của các hàm số dưới đây:

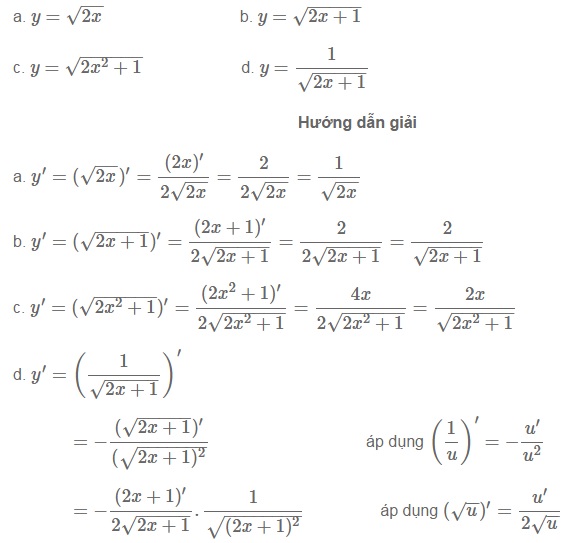
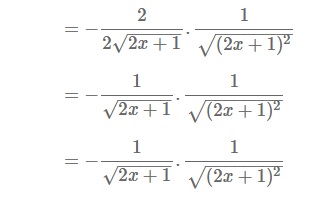
III. BÀI TẬP ĐẠO HÀM CỦA HÀM SỐ CHỨA CĂN

Câu 1: Hãy tính đạo hàm của hàm số chưa căn sau y=2x⁴−13x³+2√x−5
A.y′=8x³+x²+1/√x.
B.y′=8x³−x²−1√x.
C.y′=2x³−x²+1/√x.
D.y′=8x³−x²+1/√x.

Xem thêm : IC là gì? Cấu tạo, chức năng và phân loại IC

Lời giải​

y′=(2x⁴−13x³+2√x−5)^/⇔ y′=(2x⁴)^/−(13x³)^/+(2√x)^/−5^/ ⇔y′=8x³−x²+1/√x.

Câu 2. Hãy tính đạo hàm của hàm số chưa căn sauy=x²+x√x+1
A. −x/√1+2x−x²
B.2x+√x/2.
C.x+√x/2.
D.2x+3√x/2.

Xem thêm : IC là gì? Cấu tạo, chức năng và phân loại IC

Lời giải​

y′=(x²)^/+(x√x)^/.+1^/=2x+x′.√x+(√x)^/.x=2x+√x+1/2√x.x=2x+3√x/2

Câu 3. Hãy tính đạo hàm của hx+3√x/2.àm số chưa căn đặc biệt sau y=x²√x
A.x√x/2.
B.5√x/2.
C.5x√x/3.
D.5x√x/2.

Xem thêm : IC là gì? Cấu tạo, chức năng và phân loại IC

Lời giải​

y′=(x²√x)^/=(x²)^/.√x+(√x)^/.x²=2x.√x+1/2√x.x²=2x√x+1/2x√x=5x√x/2.

Vậy là các bạn vừa được chia sẻ các Cách tính đạo hàm của hàm căn thức và nhiều dạng bài tập thường gặp. Hi vọng, bài viết đã cung cấp cho bạn thêm nguồn tư liệu quý. Cách tính nhanh đạo hàm của các hàm số lượng giác cũng đã được thcs Hồng Thái giới thiệu rất chi tiết. Bạn tìm hiểu thêm nhé !

Đăng bởi: thcs Hồng Thái

Chuyên mục: Giáo dục

Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!

Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)