Đường phân giác là gì? Tính chất, công thức tính đường phân giác của tam giác

Cùng thcs Hồng Thái tìm hiểu đường phân giác là gì, tính chất và công thức tính đường phân giác của một tam giác.

Bạn đang xem: Đường phân giác là gì? Tính chất, công thức tính đường phân giác của tam giác

Định nghĩa đường phân giác là gì?

– Đường phân giác là của một góc chia góc đó thành hai góc có độ lớn bằng nhau. Bất kỳ góc nào cũng chỉ có duy nhất một đường phân giác. Mọi điểm trên một đường phân giác cách đều hai cạnh của góc đó và ngược lại.

– Đường phân giác trong tam giác là đường thẳng chia một góc của tam giác đó thành hai góc bằng nhau. Bên cạnh đó chúng ta còn biết được khái niệm ba đường phân giác của một tam giác. Trong một tam giác có 3 đường phân giác và chúng đồng quy với nhau tại 1 điểm. Điểm này cách đều ba cạnh của tam giác đó và được gọi là tâm đường tròn nội tiếp tam giác.

Ví dụ: trên hình tam giác có 3 đường phân giác được hạ từ 3 đỉnh A, B, C: AH, CP, BK và chúng giao nhau tại O.

Trường hợp đặc biệt hơn có thể xảy ra là đường phân giác trong tam giác cân. Trong tam giác cân, đường phân giác hạ từ đỉnh cân xuống cạnh đáy vừa là đường trung tuyến, đường trung trực, đường cao của tam giác đó.

Tia phân giác của góc  là tia  nằm chính giữa hai tia  và .

Ta có:

 là phân giác của góc  .

– Đường thẳng chứa tia phân giác gọi là đường phân giác.

– Tia phân giác của góc trong tam giác được gọi là đường phân giác của góc đó.

– Đường phân giác của một góc chia góc đó thành hai góc có độ lớn bằng nhau.

Chú ý:

– Bất kỳ góc nào cũng chỉ có duy nhất một đường phân giác.

– Trong tam giác có ba đường phân giác, chúng đồng quy tại một điểm, điểm đó gọi là tâm đường tròn nội tiếp tam giác 

Định lý đường phân giác trong tam giác

Định lý đường phân giác trong tam giác: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

Ví dụ 1: Cho △ABC có AD là tia phân giác của góc A; D thuộc BC.

Vậy ta sẽ có tỉ lệ AB/AC=DB/DC (tính chất đường phân giác trong tam giác).

Ví dụ 2:

Cho tam giác ABC có AD, AE lần lượt là đường phân giác góc trong và góc ngoài tại đỉnh A.

Khi đó ta có DB/DC=AB/AC và EB/EC=AB/AC.

Những chú ý về đường phân giác trong tam giác

Bên cạnh những lý thuyết về đường phân giác trong tam giác, chúng ta cũng cần phải để ý một vài chú ý về khái niệm này. Trước tiên, định lí về đường phân giác trong tam giác vẫn đúng với đường phân giác góc ngoài của tam giác.

Ngoài ra, chúng ta nên chú ý vẽ hình sao cho thật chính xác, đặc biệt là vẽ đường phân giác trong tam giác. Ba đường phân giác trong tam giác đồng quy tại một điểm nên mọi người cần lưu ý trong việc vẽ hình.

Ví dụ:

AE’ là phân giác của góc BAx (AB ≠ AC).

Ta có: AB/AC = E’B/E’C hay E’B/AB = E’C/AC

– Đường phân giác trong tam giác cân, tam giác đều

+ Đường phân giác trong tam giác cân hạ từ đỉnh cân xuống cạnh đáy vừa là đường trung tuyến, đường trung trực, đường cao.

+ Đường phân giác trong tam giác đều hạ 3 đỉnh đều là đường trung tuyến, đường trung trực, đường cao.

Công thức độ dài của đường phân giác

Công thức chung:

+ Công thức chung tính độ dài đường cao của một tam giác dựa vào độ dài của 2 cạnh bên đã cho và số đo góc chứa đường phân giác

+ Đường phân giác trong tam giác đều: Đường phân giác tam giác đều có độ dài bằng nhau, đường phân giác trong tam giác đều hạ 3 đỉnh cũng là đường cao, áp dụng định lý Heron ta có công thức tính đường phân giác trong tam giác đều

Ví dụ 1: Cho tam giác ABC có AB = 5cm, AC = 6cm, BC = 7cm. Tia phân giác của góc BAC cắt BC tại E. Tính các đoạn EB, EC.

Trả lời:

Vì AE là đường phân giác của tam giác ABC nên ta có:

EB/EC = AB/AC = 5/6.

Do đó theo tính chất của dãy tỉ số bằng nhau, ta có:

EB/5 = EC/6 = (EB + EC)/(5 + 6) = 7/11.

Vì vậy ta có: EB/5 = 7/11.

=> EB = 5.(7/11) = 35/11 (cm).

Ta có: EC/6 = 7/11.

=> EC = 6.(7/11) = 42/11 (cm).

Ví dụ 2: Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC.

Trả lời:

Ta có MD là đường phân giác của tam giác ABM

=> AD/BD = AM/BM (1)

ME là đường phân giác của tam giác ACM.

=> AE/CE = AM/MC (2)

Mà MB = MC (AM là đường trung tuyến)

=> AM/BM = AM/MC (3)

Từ 1, 2, 3 => AD/BD = AE/CE => DE // BC (Định lí Ta – lét đảo).

Bài tập Tính chất đường phân giác của tam giác

Bài tập Tính chất đường phân giác của tam giác có đáp án gồm các dạng bài tập về Tính chất đường phân giác của tam giác lớp 8 từ cơ bản đến nâng cao giúp học sinh lớp 8 biết cách làm bài tập Tính chất đường phân giác của tam giác.

Bài 1: Cho Δ ABC vuông tại A có AB = 3 cm, BC = 5 cm, AD là đường phân giác của Δ ABC. Chọn phát biểu đúng?

A. BD = 20/7 cm; CD = 15/7 cm

   B. BD = 15/7 cm; CD = 20/7 cm

C. BD = 1,5 cm; CD = 2,5 cm

D. BD = 2,5 cm; CD = 1,5 cm

Lời giải:

Áp dụng định lý Py – ta – go ta có: AC = √ (BC² – AB²) = √ (5² – 3²) = 4( cm )

Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )

Ta có: DB/DC = AB/AC hay DB/AB = DC/AC

Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)

hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )

Chọn đáp án B.

Bài 2: Cho Δ ABC có BD là đường phân giác, AB = 8 cm, BC = 10 cm, AC = 6cm. Chọn phát biểu đúng?

   A. DA = 8/3 cm, DC = 10/3 cm

B. DA = 10/3 cm, DC = 8/3 cm

C. DA = 4 cm, DC = 2 cm

D. DA = 3,5 cm, DC = 2,5 cm

Lời giải:

BD là đường phân giác của Δ ABC

Xem thêm : Khối C00 thi trường nào? Tổng hợp các trường đại học khối C00

Ta có: DA/DC = AB/BC ⇔ DA/(DA + DC) = AB/(AB + BC)

Hay DA/6 = 8/(8 + 10) ⇒ DA = (6.8)/18 = 8/3 ( cm ); DC = 10/3 (cm)

Chọn đáp án A.

Bài 3: Cho Δ ABC có Aˆ = 90^o, AD là đường phân giác. Chọn phát biểu đúng?

A. 1/AD + 1/AC = 1/AB

   B. 1/AB + 1/AC = 1/AD

C. 1/AB + 1/AC = 2/AD

D. 1/AB + 1/AC + 1/AD = 1

Lời giải:

Δ ABC có AD là đường phân giác

Ta có: DB/DC = AB/AC và DC/DB = AC/AB

+ AC là phân giác góc ngoài của Δ ABD

Có: AD/AB = DC/BC

+ AB là phân giác góc ngoài của Δ ADC

Có: AD/AC = BD/BC

Khi đó ta có: AD/AB + AD/AC = DC/BC + DB/BC = 1 ⇒ 1/AB + 1/AC = 1/AD

Chọn đáp án B.

Bài 4: Cho Δ ABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x ?

A. x = 14   B. x = 12

   C. x = 8   D. x = 6

Lời giải:

Δ ABC có AD là phân giác trong của góc A.

Ta có: DB/DC = AB/AC ⇒ DB/(BC – DB) = AB/AC

Hay 9/(21 – 9) = 6/x ⇒ x = (12.6)/9 = 8

Chọn đáp án C.

Bài 5: Cho Δ ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác BACˆ cắt BC tại D. Tỉ số diện tích của Δ ABD và Δ ACD là?

A. 1/4   B. 1/2

   C. 3/4   D. 1/3

Lời giải:

Đường phân giác BACˆ cắt BC tại D

Ta có: DB/DC = AB/AC = 15/20 = 3/4

Chọn đáp án C.

Bài 6: Cho tam giác ABC có AB = 4cm ; AC = 9cm.Gọi AD là tia phân giác của BACˆ. Tính tỉ số CD/BD

Lời giải:

Áp dụng tính chất đường phân giác của tam giác ABC ta có:

Chọn đáp án B

Bài 7: Cho tam giác ABC có AC = 4cm, AB = 6cm và BC = 8cm. Gọi AD là tia phân giác của BACˆ. Tính BD?

A. 4,2 cm     B. 4,8cm

C. 5,2cm     D. 5,4cm

Lời giải:

Chọn đáp án B

Bài 8: Cho tam giác ABC cân tại A có BC = 10cm . Gọi AD là tia phân giác của góc BACˆ. Tính CD?

Lời giải:

Theo tính chất tia phân giác của góc ta có:

Do tam giác ABC cân tại A nên AB = AC nên:

Suy ra : DB = DC.

Mà DB + DC = BC nên:

Chọn đáp án C

Bài 9: Cho tam giác ABC có AD là tia phân giác của góc BACˆ. Biết AB = 3cm, BD = 4cm, CD = 6cm. Tính AC?

A. 4cm     B. 5cm

C. 6cm     D. 4,5cm

Lời giải:

Theo tính chất tia phân giác của góc ta có:

Suy ra:

Chọn đáp án D

Bài 10: Cho tam giác ABC có đường trung tuyến AM và đường phân giác AD của góc BACˆ.

Biết AB = 12 cm; AC = 8cm và BC = 15cm. Tính tỉ số BM/BD.

Lời giải:

Do M là trung điểm của BC nên:

Theo tính chất tia phân giác của góc ta có:

Suy ra:

Theo tính chất của dãy tỉ số bằng nhau ta có:

Suy ra:

Do đó:

Chọn đáp án A

Bài 11: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC, khi đó  ?

Lời giải:

Đáp án cần chọn là: D

Bài 12: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Xét các khẳng định sau, số khẳng định đúng là:

A. 0

B. 3

C. 1

D. 2

Lời giải:

Vì AD là đường phân giác của tam giác ABC nên: 

Vậy chỉ có 2 khẳng định đúng.

Đáp án cần chọn là: D

Bài 13: Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?

A. 3cm

B. 6cm

C. 9cm

D. 12cm

Lời giải:

Mà tam giác ABC cân tại A nên AC = AB = 15cm

Đáp án cần chọn là: C

Bài 14: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:

A. 1,5

B. 3    

C. 4,5

D. 4

Lời giải:

Tam giác ABC vuông tại A, áp dụng định lý Pytago có: BC² = AB² + AC²

Đáp án cần chọn là: B

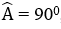
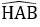
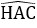
Bài 15: Cho tam giác ABC,  , AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của   cắt HB tại D. Tia phân giác của  cắt HC tại E. Tính DH?

A. 4cm

B. 6cm

C. 9cm

D. 12cm

Lời giải:

Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:

AB² + AC² = BC²

⇔ 15² + 20² = BC² ⇒ BC = 25

Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:

AB² = AH² + HB²

⇔ 15² = 12² + HB²

⇒ HB² = 81 ⇒ HB = 9

⇒ HC = BC – HB = 25 – 9 = 16

Vì AD là phân giác của tam giác ABH nên:

Đáp án cần chọn là: A

Hy vọng thông qua bài học trên, các em đã nắm rõ được đường phân giác là gì và tính chất đường phân giác của tam giác. Thầy cô chúc các em học tập thật tốt.

Đăng bởi: thcs Hồng Thái

Chuyên mục: Giáo Dục

Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!

Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)