Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
- Hạt nhân một nguyên tử fluorine có 9 proton và 10 neutron. Khối lượng của nguyên tử fluorine xấp xỉ bằng
- Viết bài văn suy nghĩ của em về tình mẫu tử trong cuộc sống (20 Mẫu)
- Lời bài hát Đố Anh Đoán Được – Bích Phương
- Hoàn thành sơ đồ dưới đây | SBT Sử 10 Chân trời sáng tạo
- Phân tích hình tượng Tnú trong truyện ngắn Rừng xà nu
Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
Các công thức đạo hàm và đạo hàm lượng giác là phần kiến thức Toán 11 rất quan trọng nhưng lại nhiều và khá phức tạp. Nếu không được luyện tập thường xuyên học sinh sẽ dễ dàng quên ngay. Bài viết hôm nay, thcs Hồng Thái sẽ hệ thống lại đầy đủ và chi tiết tất cả các kiến thức cần ghi nhớ. Các bạn xem để lưu lại nhé !
Bạn đang xem: Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
I. LÝ THUYẾT CHUNG
1. Đạo hàm là gì ?
Bạn đang xem: Bảng công thức Đạo hàm và Đạo hàm lượng giác [Đầy Đủ]
Trong giải tích toán học, đạo hàm của một hàm số thực chất là sự mô tả sự biến thiên của hàm số tại một điểm nào đó.
Trong vật lý, đạo hàm biểu diễn vận tốc tức thời của một điểm chuyển động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn.
Trong hình học đạo hàm là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Tiếp tuyến đó là xấp xỉ tuyến tính gần đúng nhất của hàm ở gần giá trị đầu vào.
2. Đạo hàm của các hàm số lượng giác là gì?
Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).
II. BẢNG CÔNG THỨC ĐẠO HÀM VÀ ĐẠO HÀM LƯỢNG GIÁC ĐẦY ĐỦ NHẤT

1. Định nghĩa đạo hàm, đạo hàm sơ cấp, đạo hàm cao cấp

2. Các quy tắc của đạo hàm cơ bản cần ghi nhớ

3. Các công thức đạo hàm cơ bản cần ghi nhớ
- Đạo hàm của f(x) với x là biến số
- Đạo hàm của f(u) với u là một hàm số
- Đạo hàm của một số phân thức hữu tỉ thường gặp

4. Bảng đạo hàm của các hàm lượng giác và các hàm lượng giác ngược
+ Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).
+ Biết được đạo hàm của sin(x) và cos(x), chúng ta dễ dàng tìm được đạo hàm của các hàm lượng giác còn lại do chúng được biểu diễn bằng hai hàm trên, bằng cách dùng quy tắc thương.
+ Phép chứng minh đạo hàm của sin(x) và cos(x) được diễn giải ở bên dưới, và từ đó cho phép tính đạo hàm của các hàm lương giác khác.
+ Việc tính đạo hàm của hàm lượng giác ngược và một số hàm lượng giác thông dụng khác cũng được trình bày ở bên dưới.

5. Bảng đạo hàm của một số phân thức hữu tỉ
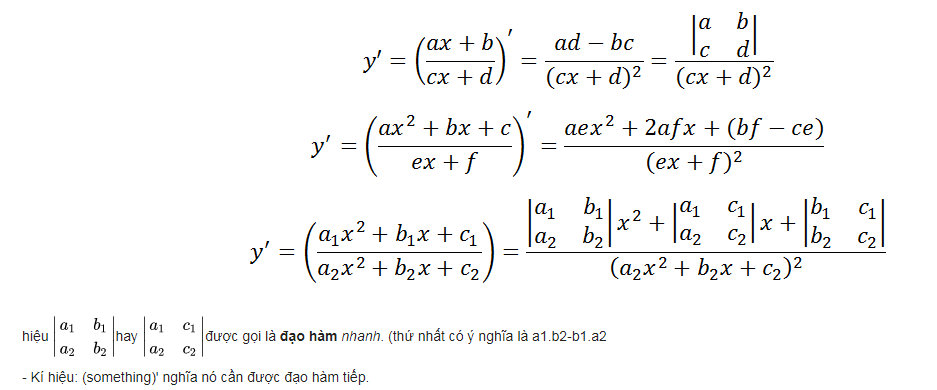
Xem thêm : Tiềm lực chính trị – tinh thần là gì? Nhân tố chính trị – tinh thần trong cuộc kháng chiến chống Mỹ
6. Bảng đạo hàm của hàm số cấp cao

7. Bảng đạo hàm và nguyên hàm

III. CÁCH TÍNH ĐẠO HÀM BẰNG MÁY TÍNH
Máy tính cầm tay là một công cụ đắc lực trong việc tính đạo hàm cấp 1, cấp 2. Tính đạo hàm bằng máy tính mang lại kết quả có độ chính xác cao và các thao tác thực hiện rất dễ dàng như sau:
Tính đạo hàm cấp 1:
Tính đạo hàm cấp 2:
Dự đoán công thức đạo hàm bậc n :
+ Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3.
+ Bước 2: Tìm quy luật về số, quy luật về dấu, về hệ số, về biến số, về số mũ rồi rút ra công thức tổng quát
IV. BÀI TẬP TÍNH ĐẠO HÀM CỦA CÁC HÀM SỐ LƯỢNG GIÁC
Bài 1:
Đạo hàm của hàm số y = 1/ (cos²x – sin²x) là :
A. y’ = 2sin2x/cos²2x B. y’ = 2cos2x/cos²2x
C. y’ = cos2x/cos²2x D. y’ = sin2x/cos²2x .
Hướng dẫn giải:
y = 1/ (cos²x – sin²x) = 1/cos2x.
Áp dụng quy tắc tính đạo hàm với (1/u)’ = -u’/u² ta được”
y’ = -(cos2x)’/ (cos2x)² = sin2x. (2x)’/ cos²2x = 2sin2x.cos²2x.
Bài 2:
Cho hàm y = cotx/2. Hệ thức nào sau đây là đúng?
A. y² + 2y’ = 0 B. y² + 2y’ + 1 = 0
C. y² + 2y’ + 2 = 0 D. y² + 2y’ -1 = 0.
Hướng dẫn giải:
Ta có y’ = -1/(sin²x/2) = -1/2 ( 1+ cot²x/2).
Do đó y² + 2y’= cot²x/2 – 2.1/2(1 +cot²x/2) = cot²x/2 – (1 +cot²x/2) = -1 nên y² + 2y’ + 1 = 0. Chọn đáp án B.
Xem thêm : Luận giải ý nghĩa tên Ngọc Anh & phán tương lai, tính cách cực chuẩn
Cách 2: Sử dụng máy tính casio.
Bước 1: Thiết lập môi trường SHIFT MODE 4.
Thay x = 1 vào y = cotx/2 ta tính được y cot 1/2 ≈ 1
Sử dụng phím SHIFT ∫, nhập hàm số y = cotx/2 với x = 1 được kết quả ≈ -1.
Do đó y² + 2y’ + 1 = 0.
Bài 3:
ính đạo hàm cấp n của hàm số y = cos2x là:
A. y(n) = (-1) ncos (2x + n π/2)
B. y(n) = 2 n cos ( 2x +π/2).
C. y(n) = 2n +1 cos (2x + nπ/2).
D. y(n) = 2n cos (2x + nπ/2).
Hướng dẫn giải:
Ta có y′=2cos(2x+π2),y′′=2²cos(2x+2π2)
y′′′=2³cos(2x+3π2)
Bằng quy nạp ta chứng minh được y(n)= 2ncos(2x+nπ2)
Bài 4:
Cho hàm số y= (x2+2x-1)/(2x-2). Tính đạo hàm của hàm số tại x= – 2
![]()
Hướng dẫn giải
Điều kiện : x≠1
Với mọi x≠1 hàm số có đạo hàm là;

Đăng bởi: thcs Hồng Thái
Chuyên mục: Giáo dục
Bản quyền bài viết thuộc Trường THCS Hồng Thái Hải Phòng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường thcs Hồng Thái (thcshongthaiad.edu.vn)
Nguồn: https://thcshongthaiad.edu.vn
Danh mục: Tra Cứu

